Special notations have been used for the following paper since the WWW does not currently support Greek characters:
B = beta
L = lambda
D = delta
T & t = theta
V = Ni
mo = initial mass
The Compton Effect and Autodynamics
by Ricardo L. Carezani
Abstract
The Autodynamics equations, when applied to the Compton Effect, yield an equation very different from the classic one. The value of h found by Ross and Kirkpatrick by extrapolating observed shift data to zero wave length is easily found using the Autodynamics equation by extrapolating to zero wave frequency. It is possible to demonstrate that the slope of the line joining two different points of value lambda (L), delta lambda (DL), determines the scattered electron Binding Energy (B.E.) corresponding to the electron orbit within the atom.
Introduction
It is well known that the collision between photons and electrons and consequent scattering has been explained by A. H. Compton(1). An application of Special Relativity yields the very simple equation:

Different experiments(2,3) demonstrated that the equation was correct within the limits of experimental errors. Nutting(4) demonstrated that the values of h were low by about 1 or 2 % with respect to the theoretical value, and attributed those low values to experimental error. Wentzel(5) was the first to point out that the values would be less if we considered the electrons’ B.E. with the nucleus, although he didn’t give an equation by which to calculate.
P. A. Ross and P. Kirkpatrick(6) were the first to propose a corrective empirical term which would explain the experimental(7) values they found. That “corrective term” as we will see below is part of the Autodynamics equation.
Bloch(8) gave a more detailed explanation theoretically supported by the Wave Mechanics.
Further, in The Marmet’s Non-Doppler Redshift section, an application to this matter yields a congruent result regarding the inadequacy of the DL from special relativity.
Recently H. Pierre Noyes pointed out (9): “As has been emphasized by Pierre Duhem, a theoretical structure in Physics is never tested in all its aspects, and as has been emphasized by Kuhn, a theory is rarely tested unless an alternative theory is proposed”.
The Compton Effect
The Autodynamics’ equations(9,10) for kinetic energy and momentum are:
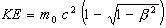 (1)
(1)
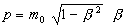 (2)
(2)
mo = electron rest mass, v = particle’s velocity, c = light velocity.
Applying these equations to Compton Effect and setting 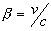 and frequency = V, we have
and frequency = V, we have
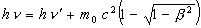 (3)
(3)
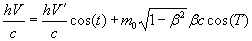 (4)
(4)
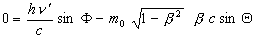 (5)
(5)
t = angle of scattered photon, V’
T = angle of scattered electron
Equation (3) yields:
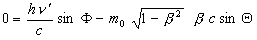 (6)
(6)
From equation (4) we have:
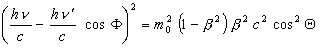 (7)
(7)
From equation (5) we have:
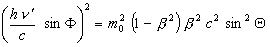 (8)
(8)
Adding (7) and (8), simplifying the right term with 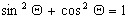 , simplifying the left term with
, simplifying the left term with 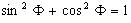 and
and 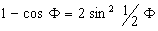 , and replacing
, and replacing 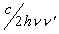 and
and 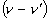 in the right term we have:
in the right term we have:
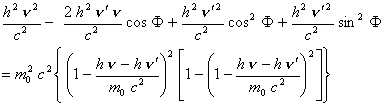 (9)
(9)
Developing the product terms and simplifying we have:
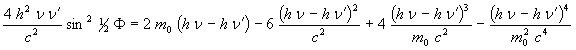 (10)
(10)
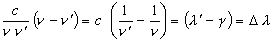 (11)
(11)
the final equation, very different from the classic one, is:
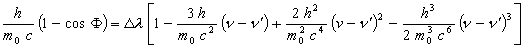 (12)
(12)
We can transform this equation for fast computer iteration. If h/moc = H and t = 90o we have:
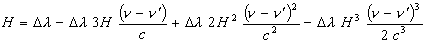 (13)
(13)
Simplifying we have:
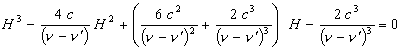 (14)
(14)
And finally we have:
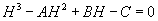 (15)
(15)
In the equation (12) or (15) the H value determines the electron energy:
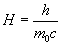 (16)
(16)
H changes to satisfy the equation (12) or (15) for different values of (V-V’), that is to say, different values of energies. When the energy increases, H decreases, and each mo of equation (16) will increase to a value equal to:
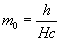 (17)
(17)
This mass value is the total electron energy. Using equations (3) and (1) the kinetic energy in eV can be calculated.
The change of H (or the equivalent DLe) given by the Autodynamics’ equation for each energy is in opposition to the old idea that the value might be the same for all experimental values (energies), and that consequently it would be necessary to modify the theoretical values of the Compton’s constant with consequent modification of Planck’s constant. However, Ross and Kirkpatrick(6) had the opposite idea. On page 673 they wrote: “It is now seen that conclusions so drawn must be erroneous, and that h/mc is to be determined by extrapolating observed shift data to zero wave-length”.
The proposed extrapolation is replaced in Autodynamics by “to zero wave-frequency”, that is to say, when the wave length increases to Ï, (V-V’) will tend to zero and in the limit DLexperimental will be equal to DLtheoretical.
DLexper. is given by a set of values, or, at least, two of them, which represent the scattered electrons energies from the same orbital level within the atom. Those electrons energies will be reduced by the electron B.E. with the nucleus.
DLexper. is easily calculated looking at Fig. 1.
Figure 1
Showing how to calculate DL experimental.
For Autodynamics the slope of the straight line that joins P1 (L1, DL1) and P3 (L3, DL3) represents the electron B.E. value if we extrapolate each energy to the maximum level of DLtheor., discounting the work function (W.F.) proportion and subtracting the original energy.
It is interesting that the Autodynamics’ equation, starting with a secure B.E. value, permits calculation of the expected experimental values of L1, DL1 and L3, DL3 and others.
In Fig. 2 taken from reference (6) a few different lines are drawn which represent the resulting values obtained by applying the Autodynamics’ equation (12) or (15).
Figure 2.
This figure is Fig. 4 of reference (6) where we can read: Wave-length shift in Angstroms for ninety-degree scattering vs. square of incident wave-length in Angstroms. Single circles represent observed scattering by beryllium; double circles by carbon. Solid line are the straight lines which best fit the data and possess the intercept h/mc. Dotted lines indicate the requirements of Bloch’s theory. The lines A, B, C, D, E, C1, and F are explained in the text
Using the more secure experimental values given by Ross and Kirkpatrick(6) for Carbon (line C) the equation 12 or 15 gives the values shown in Table 1.
| P1 | P2 | P3 |+——–+—————-+—————-+—————-+| L | 4.35 10^-11| 4.96 10^-11| 6.31 10^-11|| V | 6.891780 10^18 | 6.044202 10^18 | 4.751069 10^18 || DL | 2.388 10^-12| 2.379165 10^-12| 2.355608 10^-12|| H(DLe) | 2.396582 10^-12| 2.401289 10^-12| 2.407387 10^-12|| Ec (eV)| 1.485284 10^3 | 1.145717 10^3 | 7.080935 10^2 ||DLexper.| 2.417335 10^-12| 2.417434 10^-12| 2.417335 10^-12|| Et | 1.509111 10^3 | 1.168419 10^3 | 7.293459 10^2 || Et-BE | 1.504190 10^3 | 1.164623 10^3 | 7.269998 10^2 ||B.E.(eV)|18.9062942378 |18.9062942378 |18.906294239 |+——–+—————-+—————-+—————-+
Table I
The explanation of the values is in the text. Et = E(DL theor.), Et-BE = E(DL theor.) – WF’s proportion. h theoretical = 6.626176 10^-34 J.s, mo = 9.109534 10^-31 Kg, c = 2.99792458 10^8 m/s, DLtheor.= 2.42630896604 10^-12 m.
To obtain a B.E. value equal to 18.906294 eV (2s level) for the three points P1, P2 and P3 of Fig. 2 it is necessary to change the experimental value of DL3 = 2.356 to 2.35560893558 10^-12, that is to say, only 391 parts per million, and P2 value of 2.379 10^-12 to 2.37016598753 10^-12.
Decreasing the P1 value to 2.387 10^-12 and consequently adjusting the others, the B.E. increases to 19.530866 eV. The experimental value(11) is 19.39 eV., then the P1 value is between 2.388 10^-12 and 2.387 10^-12 though more close to the last one. The Ross and Kirkpatrick values are very good.
It is possible to see that each value of H or DLe is different in each point but the DLexper. value is 2.41730315654 10^-12 when it is calculated with the values of P1 and P3. The value of DLexper. at P2 position has a very little difference (99 parts per million) when it is calculated with the values at points P1 and P2. This demonstrated that it might also be necessary to change the value at point P1, or to modify all three points accordingly to have equal values of DLexper. and the three values of B.E., respectively.
The line C1 represents the proportion of W.F. for each point of line C. Line D represents the values of L1, DL1 and L3, DL3 calculated taking the known value of Carbon, 2p level, B.E. equal to 11.3 eV. Line B for B.E. of 111.5 eV for Be, 1s level. Line A for B.E. of 282.4 eV for C, 1s level.
Because the Ross and Kirkpatrick values for the Be are uncertain, line E represents the values of L1, DL1 and L3, DL3 calculated with the known value of B.E. for Be, 2s level, equal to 9.32 eV and it is close to the value expected by the former.
Line F represents the values shown in Table II for very small energies. It is possible to see that H (DLe) of each points P1 and P3 are very close – and also DLexper.- to the theoretical value of DL. W.F. was supposed to be equal to zero and the B.E. value is only symbolic(free electron).
| P1 | P2 |+———+———————–+———————-+| D| 3.8 10^-8 | 4.0 10^-8 || V| 7.889275210526 10^15 | 7.49481145 10^15 || DL| 2.35743989278 10^-12 | 2.35 10^-12|| H(DLe) | 2.42630656378 10^-12 | 2.42630656668 10^-12|| Ec(eV)| 2.02679462856 10^-3 | 1.82341539579 10^-3 || DL exper| 2.42630659262 10^-12 | —— || B.E. | 5.9209796 10^-5 | 5.9209789 10^-5 || (V-V’) | 4.8940364123 10^11 | 4.40294305397 10^11 |+———+———————–+———————-+
Table II
Values for Line F of Fig.2
The equation for t = 180o also demonstrated that H (DLe) tends to 2DLtheor. when the energy tends to zero.
The Forward Emission
If t = 0, cos t = 1 and (1 – cost) = 0, the equation (12) will be
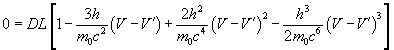 (18)
(18)
As DL is not zero the other term must be zero.
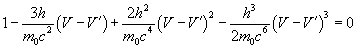 (19)
(19)
This equation gives the photonic reemission in the forward direction. As L’ is bigger than L and, at the same time, the photon reemitted is in the same straight path of the incoming photon it is possible to interpret this as a redshift.
Marmet’s Non-Doppler Redshift (13)
The Canadian Astrophysicist Paul Marmet is the author of a theory that explains the redshift by taking the intergalactic medium into account.(Gas in the intergalactic space).
The incoming photon energy (hV) will be “absorbed” by the electron-proton system of hydrogen. This interaction will transfer the photon momentum to the electron in the direction of the photon. This momentum transfer to the electron will accelerate it so that it will lose some energy by radiation, (called breaking energy or “bremsstrahlung”) according to the electrodynamics principle.
After a finite interval of time (about 10^-16 second) a photon that has lost a very small fraction (loss of about 10^-12 hV) of its initial energy will be reemitted in the forward direction.
The Special-Relativity-Compton-Effect equation does not explain the phenomenon, because the equation ( L L) is equal to zero when t = 0.
On the contrary, as was explained before, equation (19) gives values to calculate the red shift, or given this, to calculate the energy transferred to the electron within the atom.
Discussion
The Autodynamics’ equations apply when there is decay, that is to say, autotransformation of mass into energy. How is that phenomenon present in the Compton Effect?
The incident photon, the electron and the scattered photon form a closed system. The incident photon (hV) collides with the electron that has its own energy (mo+m’) and direction of movement, forming a unique “particle” that will be called “photon-electron”. This “particle” will decay with emission of a photon (hV’) and the rest of the “particle” mass will decay to an electron.
Conclusion
The Autodynamics equation for the Compton Effect is more complete than the classic one and resolves many doubts discussed in the past.
The author of this paper thinks, however, that the equation needs more detailed research and special experimentation by specialists in the matter to investigate these results. Autodynamics also determines the energy and direction of the electron before the collision with the incident photon.
Acknowledgments
The Author thanks Kourosh Bouturabi and Tina Perjol for assistance in preparing the English version of this paper, and Cynthia Kolb Whitney for a few final corrections. The Author’s gratitude also goes to Abbas Saffar and Tina Perjol, owners of Deck-Aid Co., who facilitated the computer capabilities to make all the calculations needed. Thanks to P. Marmet who clarified the phrase explaining his theory. Thanks to both reviewers, who gave a good opinion of the paper, and especially to those who made corrections to the English and improved the paper technically.
References
- A.H. Compton. Phys. Rev.,21,483 (1923).
- H.M. Sharp. Phys. Rev.,26,691 (1925).
- H. Kallmann and H. Mark. Naturwissenshaften,3 (1925).
- F.L. Nutting. Phys. Rev.,36,1267 (1930) and references.
- G. Wentzel. Zeits f. Physick,43,1,779 (1927).
- P.A. Ross and Kirkpatrick. Phys. Rev.,46,668 (1934).
- P.A. Ross and Kirkpatrick. Phys. Rev.,45,223 (1934).
- F. Bloch. Phys. Rev.,46,674 (1934).
- D.R. Walz, H.P. Noyes, R.L. Carezani. Phys. Rev. A,29, 2110 (1984). The conclusion espoused in the paper by H.P. Noyes is irrelevant because the electrons receive external energy from the Klystrons’ electromagnetic field, confirming the Bertozzi experiment(12) and the Special Relativity equation for kinetic energy. It is impossible then to compare one equation against the other because Autodynamics applies to decay cases.
- R. L. Carezani. Physics Essays 1,269 (1988).
- K. D. Sevier, Atomic Data and Nuclear Data Tables. 24,323(1979).The data was really sent to me by the Editor, Angela Li-Scholz, to whom I am grateful.
- W. Bertozzi. American Journal of Physics,32,551 (1964)
- P. Marmet. Physics Essays 1,24 (1988). IEEE Transactions on Plasma Science 17,238 (1989).
This is the paper sent to the PHYSICS ESSAYS after the reviewer criticism. March 7, 1992. Sent again, after two new corrections by the two referees on August 27,1992 and January 21, 1993 with Marmet reference in introduction.