by Ricardo Carezani
As with many powerful yet elegant theories, the derivation is often the most powerful argument for the theory itself. Such is the case with Autodynamics. Although it is impossible to discuss the background necessary to adequately set up the AD derivation in this small article, the math is quite simple and elegant.
Discussing in detail the Galilean coordinate transformation principle and comparing it with the Lorentz-Einstein transformation of frames in relative motion, the author of AD demonstrated that it is possible to simplify the Lorentz equations by recognizing that one of the two coordinate systems used by Lorentz and Einstein were superfluous. Not only was one coordinate system superfluous, but the relationship between the Lorentz coordinate systems (one for the object and one for the observer) was arbitrarily fixed by Einstein by setting their relative velocities equal in the acceleration derivation and introducing a problem in the velocity sum equation.
SR: 2 coordinate systems
Below is the universal system of frames for relative movement.
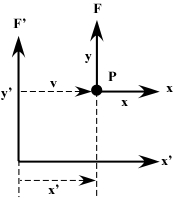
Figure 1 System of coordinates
We will first find the velocity v’ of an object with respect to the observer using the Lorentz equations. But it is important to note that the object is at rest with respect to its coordinate system F, and in motion with respect to the observer in F ‘ (this becomes very important further on).
The Lorentz equations are:
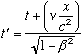
(1)
(where 
, v = particle velocity, and c = light velocity)
SR Velocity
The Lorentz equations in differential form, are
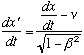
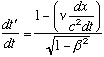
(2)
In order to find the velocity v’ we need to divide 
by 
:
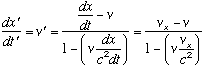
(3)
This equation was obtained working with two frames in relative motion and with a point P at rest in frame F (see above figure). Yet equation (3) has 3 velocities even though it must only have 2.
What is remarkable, is that the velocity vx appears spontaneously through the mathematical operation of the derivative from the coordinate x in equation (1) to the derivative dx/dt in equation (2). This innocent operation has no physical meaning. There is no energy to move point P (originally at rest in frame F) with respect to the F coordinate system. This is the reason why the SR sum velocities equation fails to maintain momentum and energy conservation when the equation is applied to a dynamic physical phenomenon observed by observers in two relative frames in motion.
SR Force
Now that we have the velocity v’ for the object with respect to the observer, we now can derive the SR equation for force.
In frame F, force is
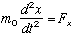
(4)
In frame F ‘, force is
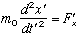
(5)
We need to find the acceleration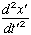 
. Using the chain derivative, we now need to take the derivative of v’ to get acceleration using equation (3).
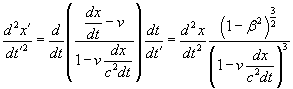
(6)
and given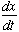 
= vx. we obtain the acceleration:
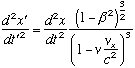
(7)
But in order to obtain the well known SR formula
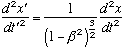
(8)
it is necessary to set vx = v.
Once again, this simplification has no physical sense. There is no reason for setting these two velocities equal. To confound the matter, the exponent 3/2 in equation (8) does not end up matching the 1/2 in target Lorentz’s equation. In other words, even with the strange assumption that vx must equal v, it still does not match the desired Lorentz exponent.
An even more strange phenomena in Einstein’s derivation is the question of why he didn’t set the velocities equal to each other back in equation (3). The problem is if he did, the result would be very strange indeed: either 0, or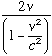 
. This emphasizes again the utter irrelevance of setting the two velocities equal. In reality, there are an infinite number of choices for v and vx (either taking on any value between 0 and c).
AD
AD: 1 coordinate system
These problems never arise in Autodynamics because there is only one frame of reference.
There are two ways to derive the AD equations for a system in relative motion. One involves using Galilean transformations without using calculus thus avoiding any spontaneous generation of velocity requiring physical energy. The result leads to a simplification of the Lorentz time dilation equation and the observers coordinate position. This however, is too long and involved for this type of article.
The second way to derive the AD equations is shorter and more classical.
Returning to the figure for frames of reference, we see below that AD “collapses” the two SR coordinate systems into one.
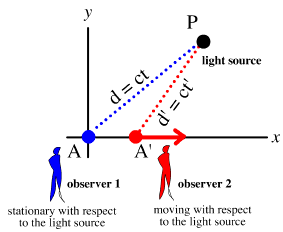
In SR, position and time in one coordinate system are a function of position and time with respect to another coordinate system:
(x’,y’,z’,t’) = f(x,y,z,t)
(9)
Without the extra coordinate system, AD describes position and time for one frame of reference as only a function of time:
(x’,y’,z’,t’) = f(t)
(10)
To remain consistent with the simultaneity problem of the relationship of two observers viewing the same object, let us describe the coordinates of both observers for AD:
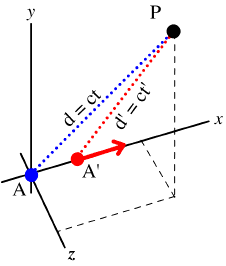
(11)
(12)
Because Einstein’s equations had four variables x, y, z, & t, he had to solve four equations simultaneously. AD on the other hand has only one variable t, and thus has to solve only one equation.
Both AD and SR assume y & z and y’ & z’ are parallel respectively for both observers and therefore equal:
y’ = y
z’ = z (13)
But unlike SR, the AD function is dependent on only one variable t, and thus x’ and t’ must be related by one coefficient a:
x’ = avt
t’ = at(14)
Substituting (13) and (14) into (12) and solving for a:
(15)
(16)
Given that the coefficient for t2 in (11) is c2, and the coefficient for t2 in (16) is a2c2 -a2v2, then we set those coefficients equal:
(17)
(18)
Substituting a in equation (14), we get the AD equations:
(19)
In AD, these are called the “Simplified Lorentz Equations”.
AD VelocityContinuing, we find the velocity of the observer in frame F’ by taking the derivative of equation (19),
and calculating v’ by dividing the above two equations:
The result is that v’ = v: the observer velocity IS the object velocity. This is not surprising given that in AD, frame F is collapsed onto F’ and therefore the velocity of the object is equal to the velocity of frame F with respect to F’ before collapsing. |
AD Force
Taking the derivative of equation (21) yields the acceleration:
(22)
Given the classical definition of force
(23)
we substitute the result of (22) into (23) and get
(24)
Thus, the mass in motion must be
(25)
This makes complete physical sense: when energy is expended, mass is expended! This is one of the elegant mathematical descriptions of the AD theory.
AD Kinetic Energy
First we start out with rest mass energy:
(26)
Next, we describe energy of a particle that begins to move from a decay process:
(27)
Substituting equation (25) for mass and (26) for energy, we get
(28)
(29)
The equations for kinetic energy (29) and mass (25) are coherent: when the mass decreases, the kinetic energy increases and there is energy conservation.