by Ricardo Carezani
The total energy in AD will be conceptually different from SR. We saw that in SR W = mo c2 + E, where E is the electron KE. In AD,E could be the KE or simply the energy absorbed or emitted by the electron. This is possible for two reasons.
First:
The principle of energy absorption-energy emission or decay.
Second:
An atom only absorbs the same quantum of energy that it can emit.
E preferably represents this type of quantified energy. AD enables the momentum equation to be written directly in polar coordinates,
(32)
(33)
or to create a Lagrange function, taking the partial derivative as a function of 
2 in polar coordinates
(34)
The Lagrange function is written as
(35)
Taking the partial derivative, we have
(36)
(37)
As will be seen later, using equations (30) and (31) is equivalent to using equations (34) and (35), because the terms are equal in the sum and they are eliminated.
The total internal energy W is equal to the electron rest mass energy plus the electron potential energy
(38)
As will be demonstrated later, this equation, showing the variable separation, can be written as follows
(39)
As will be shown in Appendix A10, the second part of (39) is equal to mo c2. Rearranging and squaring both sides, we have
(40)
Reworking the equation, we find
(41)
As will be seen later, the 
term introduces a new quantum number, that leads to the four quantum numbers of Dirac’s equation.
Making
(42)
(43)
(44)
The equation showing the variable separation is
(45)
Remembering that
(46)
and introducing the Sommerfeld fine structure constant 
,A, B and C take the following form:
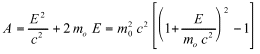(47)
(48)
(49)
Applying the theorem of residues, a similar equation to equation(27) is found, with the only difference that divides the result.
(50)
Equating the second member to n2 h and replacing the constants by their values in equations(47), (48) and (49) and reworking the equation yields
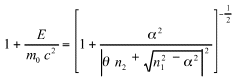(51)
Remembering that
(52)
(53)
and taking into account equations (32) and (33)
(54)
We have now four quantum numbers, n,n1, n2 and r. Changing the notation, defining n1 /r = p and n = n1 + n2 = p + l +1 and l + 1 = j + 1/2, the equation is
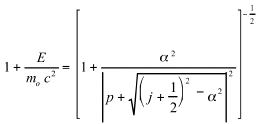(55)
This is the original Dirac equation, found via wave mechanics with four wave functions in an electromagnetic field, and considering the spinning magnetic electron.
Developing 
2to a second degree, the final equation, equivalent to equation(31) is
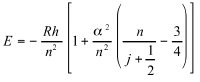(56)
It is interesting that this simple application of AD directly yields Dirac’s equation, originally obtained by a complex mathematical derivation.
Apparently, the AD treatment of the Bohr atom needs to take into account the electron magnetic momentum. We say apparently, because the participation of , that represents the vector momentum of the electron around its orbit, could be equivalent to the Dirac’s equation. In this case, it should only be necessary to introduce the spin of the electron into the equations.
End Bohr