Muon Decay
Physics Essays – Volume 5, number 1 – March 1992
The Muon Decay muon+ -> e+ e+ e+ and Autodynamics [l]
by Ricardo Carezani
Abstract
A brief explanation of autodynamics principles is given. The autodynamics equations are explained, and their application to muon decay is analyzed. Autodynamics can explain the results obtained at SLAC and CERN. The author concludes that the problem of muon and pion decay remains to be resolved by the experimenters.
Key words: autodynamics equations, muon decay, experiments of CERN and SLAC.
1. INTRODUCTION
In the last years many theoretical and experimental papers about muon and pion decay have been published. Those publications that are related to the neutrino propose various hypotheses to explain experimental results. The two comments below are from among many that illustrate the neutrino problem.
The question is now in the hands of the experimenters. Of theories we have plenty – so many that no matter how reality turns out, one will accommodate it. But within the next year, we will have enough to rule out a very large part of the speculation … assuming they really exist [1]
After more than thirty years of experiment, the nature of the Neutrino is still an extremely elusive subject. … Not much progress has indeed been made since that time… we are still dealing with the same problem. [2]
The ideas previously proposed are based upon the equations of special relativity, which are applied to particles that receive energy [3-5] from the external medium (the “cannon ball”). Those equations are also used for cases of decay, such as when there is autotransformation of matter (mass) into energy, a phenomenon that does not receive energy from the external medium, but rather has only its own rest mass energy. A new idea, no, a “new physics,” although “beyond the standard model,” [6] is proposed by autodynamics.
2. AUTODYNAMICS
The autodynamics equations, whose origins are explained in the Endnotes, have precisely the concept of autotransformation of matter (mass) into energy and are shown in Table 1, taken from Ref. 3 (see also Endnote 2) and 17.
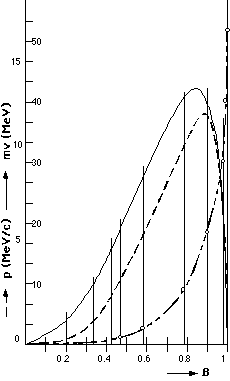
The momentum (p) equation shows that momentum first increases with increasing velocity of the particle, attaining a maximum value at the speed of 0.7c, then decreasing beyond that, although the velocity constantly increases.
The kinetic energy (E) equation shows that the energy will increase to a maximum value that is the same value as the energy accumulated in the particle when it is at rest (mass energy).
The principle of conservation of momentum and energy is maintained and the equation relating energy to momentum becomes
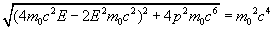 (1)
(1)
In the muon decay case, the maximum energy available is 106 MeV with a concurrent event of three particles. The three particles then take arbitrary values of mass energy mo1, mo2, mo3, then sum of which is always mo:
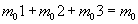 (2)
(2)
Independently, each particle must satisfy Eq. (1):
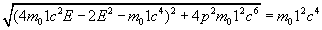 (3)
(3)
and two similar equations for particles 2 and 3 to satisfy Eq. (2).
From the equation of kinetic energy,
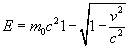 (4)
(4)
where, by setting B (beta) = v / c,
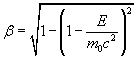 (5)
(5)
motion mass is
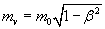 (6)
(6)
and momentum is
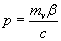 (7)
(7)
3. APPLICATION TO CASES OF MUON DECAY
If B a mo are known in Eq. (4), then E can be found. In Eq. (5), E is unknown as kinetic energy, but it is assumed that E is the part of mass energy that particle 1 takes from the total mass energy available (106 MeV for the muon) in the way that E1 = m01 c^2, and the combination of the three events simultaneously satisfies Eqs. (1) and (2), where the kinetic energy must be calculated with Eq. (4), and where mo becomes mo1, mo2, and mo3, respectively.
m01/m02/m03 B Sum E Sum p Sum E Sum p mv ======================================================= 1/3 mo 0.74535 11.777 17.557 23.555 1/3 mo 0.74535 11.777 17.557 35.333 52.671 23.555 1/3 mo 0.74535 11.777 17.557 23.555 ======================================================= 50 0.84956 23.584 22.427 26.415 40 0.78251 15.094 14.488 41.094 49.093 24.905 16 0.52830 2.415 7.176 13.584 ======================================================= 60 0.90093 33.962 23.458 26.037 30 0.69209 8.490 14.994 44.867 45.629 21.509 16 0.52830 2.415 7.176 13.584 ======================================================= 60 0.90093 33.962 23.458 26.037 40 0.78251 15.094 19.488 49.396 44.824 24.905 6 0.33166 0.339 1.877 5.660 ======================================================= 70 0.94056 46.226 22.360 23.773 30 0.69209 8.490 14.994 55.056 39.231 21.509 6 0.33166 0.339 1.877 5.660 ======================================================= 80 0.96945 60.377 19.023 19.622 20 0.58460 3.773 9.485 64.490 30.386 16.226 6 0.33166 0.339 1.877 5.660 ======================================================= 90 0.99854 76.415 13.429 13.584 10 0.42400 0.943 3.840 77.698 19.146 9.056 6 0.33166 0.339 1.877 4.764 ======================================================= 95 0.94460 85.141 9.805 9.858 6 0.33166 0.339 1.872 85.716 13.123 5.660 5 0.30350 0.236 1.446 4.764 ======================================================= 100 0.98839 94.339 5.651 5.660 3 0.23622 0.688 94.509 7.028 2.915 3 0.084 0.688 2.915 ======================================================= 104 0.99982 102.037 1.961 1.962 1 0.13703 0.009 0.135 102.056 2.233 0.990 1 0.13703 0.009 0.135 0.990 =======================================================
For massive neutral particles, xh, theta, with subsequent decay -> e+ e-, the papers of interest include Refs. 7 and 8. Attention will be given to two papers (9, 10) that are searching for the same thing, working in the same way, the results of which are presented in a very simple graphical form.
As a matter of fact, three concurrent events can each take 1/3 of the total mass energy as a lower limit, because any other combination will increase the total kinetic energy as can been in column Sum E of Table II. The upper limit is reached when all the mass energy available is converted to only a particle: positron, electron, or photon.
Figure 1(b), taken from Ref. 9, has the values of Ref. 10 added. The solid line joins the points that represent the values calculated with Autodynamics equations, as listed in Table II.
For Autodynamics, the vertical axis represents the sum of the absolute value of each vector momentum Summation |pi|, i = 1, 2, 3 and simultaneously the motion mass sum. The horizontal axis represents the energy sum, summation E, for each correlation vector momentum sum.
The values of Table II have been calculated with mo = 106 MeV for m01, m02, and m03, the portion of mass energy that each particle takes from the total mass available. The values of points in Fig. 1(a) were obtained with different criteria, as will be explained below.
Until now, the conservation of momentum in Autodynamics could take here a statistical meaning. In other words, it is not necessarily an isolated event that has to satisfy conservation of momentum, although it is not excluded from the instant when many concurrent events (decay) satisfy the principle of conservation of momentum, as it is shown and explained in Fig. 1(a).
While momentum is not conserved in many decays, conservation will be statistically realized in space or time.
Another solution to maintain momentum conservation is available through a selection rule, which makes a decay possible when the ratio of mass occurring within a concurrent events results in three vector momenta that satisfy the conservation of momentum requirement.
From the moment that the autodynamics momentum increases to a maximum value, after which it decreases, as shown in Fig. 2, it will always be possible to have a concurrent event with three particles where the vector sum of the momentum is equal to zero. Only a value in Table II, Summation E = 35.333 MeV, satisfies conservation of momentum, but in Fig. 1(a) there are other points that fulfill that principle.
 The experimenters of Refs. 7 and 8 searched for emission of neutral particles xh or theta, but no evidence of these particles was found.
The experimenters of Refs. 7 and 8 searched for emission of neutral particles xh or theta, but no evidence of these particles was found.
In Autodynamics the particles are electromuons, where the muon is defined as an electron of mass 207 times larger. The actual masses of the particles (motion mass) are shown in column mv of Table II.
The Autodynamics equation for electric charge shows that it is a function of the particle’s speed, if the phenomenon really exists.{3} The mass-to-charge-relation must be conserved, because the ratio was confirmed by experiment.
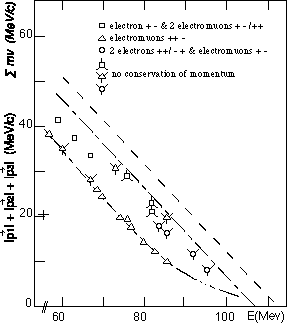
For example, taking m01 = 60 MeV, the actual mass of the particle is mv = 26.037736 MeV. With a velocity of Beta = 0.900931, an electromuon will have a mass-to-charge relation of 117.41682. In Autodynamics the ratio between mass and charge is
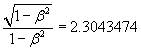
but since the motion mass of the particle is
26.037736 MeV / 0.511 MeV = 50.95443
time bigger than the electron mass, the mass-to-charge ratio will be
2.3043474 x 50.954478 = 117.41682.
This is the same value given by special relativity when the electron energy is 60 MeV, although the electron velocity is now B = 0.99999643.
In an electromagnetic field the “particle” (electromuon) looks like a positron or an electron, although the electromuon travels more slowly than the electron at the same energy.
In Autodynamics the sum of kinetic energy and motion mass is constant and always equal to the particle’s rest mass energy. Starting from the interesting idea of Refs. 7 and 8, although taking it as a probability of decay, four cases could happen in muon +,- decay: (1) in three electromuons; (2) a positron or electron and two electromuons,; (3) two positrons and an electromuon; and (4) two positrons and an electron.
Consequently, the conservation of momentum will depend upon the ratio of its energy to its momentum.
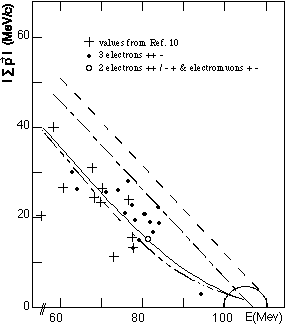
Figure 1(a) represents the value of chance combinations that satisfied the cases defined above, and they were calculated with the idea of Refs. 7 and 8, taking mot – mo1 = mos = mo2 + mo3.
To calculate the kinetic energy and momentum of particles 2 and 3, it is necessary to consider that they are only related to mos. The calculated value with emission of a positron or electron was made with the same criteria, but taking mo1 with any value up to half of the muon mass (53 MeV).
The conversation of momentum will be satisfied in the majority of electromuon cases, although exceptions are pointed out in Fig. 1(a). The conservation of momentum will not always be satisfied, individually, when there is emission of a positron or electron and two electromuons. The condition will always be fulfilled with the emission of two positrons and an electron, which represents the extreme case of autotransformation of muon mass to the maximum kinetic energy of the particles.
In Figs. 1(a) and 1(b) the dotted and dashed lines represent the maximum energy available in the way that Sum E + Sum mv = mo = 106 MeV. It is possible to see in Fig. 1(b) that the majority of the experiment points are within the limits of the two lines, especially the points of Ref. 9. In Fig. 15(b) of Ref. 6 the larger proportion of points (8835 prompt events for muon+ –> e+e+e-) is within two lines.
 Assuming that the positron takes half of the muon energy and the other half is consumed by symmetrical decay in another positron and electron, each with a quarter of the muon mass energy, then the positron with the larger energy will correspond to the maximum electron energy in the spectrum. Taking the last muon mass published {11} the maximum kinetic energy will be equal to (105.6/2) – 0.511 = 52.289 MeV and 25.889 MeV for each particle: the electron and the positron. These values can be calculated with Eqs. (4) and (5).
Assuming that the positron takes half of the muon energy and the other half is consumed by symmetrical decay in another positron and electron, each with a quarter of the muon mass energy, then the positron with the larger energy will correspond to the maximum electron energy in the spectrum. Taking the last muon mass published {11} the maximum kinetic energy will be equal to (105.6/2) – 0.511 = 52.289 MeV and 25.889 MeV for each particle: the electron and the positron. These values can be calculated with Eqs. (4) and (5).
The value of 52.289 MeV is equal to the maximum experimental value of 52.3 MeV given in Ref. 7 and obtained from Bryman et al. {12}
The experimenters of Refs. 9 and 10 have found extreme values of Sum E = 5 MV and Sum E = 85 MeV (with one exception in Ref. 9) and in coincidence with Fig. 15(b) of Ref. 6. These values suggest that the muon decay involves selection rules regarding mass ratio and the kind of particles emitted.
Autodynamics can explain the apparent loss of energy in all decay cases: in U238 decay, where the experiment values are lower {13,14} (163 MeV and 177 MeV) than the theoretical value {15} of 200 MeV, in the RaE {16} (special relativity equation), but where the calorimetric test gave 0.36 MeV, the value given by the Autodynamics equations. {17} Autodynamics can also explain the capture of K electrons {18} by vBe7 to produce 3Li7.
4. CONCLUSION
Autodynamics theory can explain the muon decay phenomenon by applying conservation of energy.
This analyst believes that the problem of muon and pion decay remains in the hands of the experimenters, especially those of Refs. 6, 9, and 10 because they have the data and the equipment that could determine whether the electron and positron are really those particles, or if they are electromuons, or electromuons with subsequent decay as shown in Fig. 3.
Acknowledgment
The author wishes to express his appreciation to Thomas E. Phipps, Jr., for recommending an earlier paper {17} for publication. The author also thanks Chandos A. Rypinski. Special thanks to the two anonymous reviewers, who with their comments and critiques, heed the author to understand the difficulties that readers may find regarding the Autodynamics concept.
ADDENDUM
One of the two reviewers in a second revision of this paper pointed out that “…the theory of Autodynamics is not described in detail and thus the author and three referees become entangled in circular arguments.”
The reviewer did not ask for an outline of the theory of Autodynamics, and in this paper we are not espousing or discussing Autodynamics theory. We only question where the Autodynamics equations can explain the muon decay phenomenon. The reviewer continues: “there are several points of the article which will come in conflict with general arguments. For instance (1) the variation of charge with velocity will lead to charge violation. For instance, take two charges of equal and opposite charge moving with constant velocity relative to each other. The moving charges have a smaller e = eo (1 – v^2 / c^2), and in the rest frame of one charge the total charge is a little positive; in the rest frame of the other charge it looks a little negative.”
Autodynamics does not have two frames in relative moment. This was said at the beginning of the Endnotes. The reviewer is in a special relativity mind-set. To apply the concepts of autodynamics, the mind-set must change. This point cannot be debated here. But we ask the reader, “who is adding the two electric charges?” An observer on an absolute system? Again, see Endnote 3.
“(2) When mo = 0, then the equations on p. 17 [Table I] do not apply. What should one do with neutrinos?” If we replace the Autodynamics equations with the special relativity equations on p. 17 [Table I], nothing changes. The equations “apply” when mo = 0. All values are zero except, of course, e; E = 0, m = 0, KE = 0, p = o. special relativity equations do not apply to neutrinos. Can the reviewer explain what happens with the kinetic energy of the neutrinos of rest mass equal to 30 eV (the Russian neutrinos) or equal to 1000 eV or 2000 eV (the Canadian neutrino) if traveling to light velocity?
“(3) If one should use the kinematics of relativity for particles in motion, then this theory is superfluous.” This point is not clearly understood. It is possible to apply special relativity for some particles in motions when receiving energy from the external medium and to apply Autodynamics for other particles in motion coming from a decay phenomenon.
The other reviewer pointed out, “First, current theory does handle the dynamics of the decay Zo ->e+e- (and similar decays) within the framework of special relativity. Note that there are no neutrinos in this decay, so the existence of neutrinos is not a question in studying the dynamics of this decay.”
The present author did not invent the neutrino. On the contrary, he is pointing out that many decays (not only the muon decay) are explained without neutrinos. The present author cannot comment on the decay of Zo either “within the framework of special relativity” or Autodynamics, because the reviewer did not give values and references. The author is now working on “nucleus-nucleus collision” with the “missing momentum” explained by Autodynamics, decays without neutrinos with “missing mass”, and the application of Autodynamics equations to the Bohr atom (hydrogen), with the positive collaboration and participation of other colleagues.
“Second, the difference in the energy or momentum measuring techniques of the crystal box and Sindrum experiments is a problem for the author. Special relativity and Autodynamics relate energy to momentum very differently. The crystal box measures energy, Sindrum measures momentum.”
The equipment used in Ref. 9 (Sindrum collaboration, Fig. 1) does not measure momentum. That device only measures the curvature of the particle’s path. The charged particle follows a curved line because it is obliged to do so by the electromagnetic field through which it is traveling. That curved line does not measure momentum. The momentum value will depend, first of all, on the equation used to calculate it: Newton’s , Einstein’s, Carezani’s, or rather Autodynamics.
Second, to calculate the velocity needed to calculate the momentum, it is necessary to know that particles rest mass and its electric charge. If the velocity is known, it is still necessary to know the particle rest mass. The reviewer continues: “When the experiments are compared within the framework of special relativity, their results are compatible. The simple overlaying of the results of the experiments’ data in the author’s Fig. 1 indicates that the author has not used his theory of Autodynamics to properly combine the results within his own theoretical framework.”
The reviewer is probably referring to Fig. 1(b). The results combine inherently, not by the choice of the author. The two experimental results are given within the framework of special relativity, which is explained as follows: if Sindrum has the momenta, of course it also has the energies. If the crystal box has the energies, of course it also has the momenta. A calculated momentum of 40 MeV/cc, for example, is the same when it is calculated with the results of the crystal box or the Sindrum collaboration. The authors used the same special relativity equations. It is possible to put the results in the same system of coordinates, because the units are the same, MeV/c. The same is true for Autodynamics, because the values are also given in units of MeV/c independently of the equation used. The other axis represents energy, and of course, it is the same thing. This is because the units are the same: MeV. The only difference is that special relativity needs the neutrino to maintain the energy and momentum conservation principle, and Autodynamics does not need the neutrino. The reviewer continues:
“On p. 8 [Sec. 3] he states that the time of flight of electromuons will be quite different from electrons. This is a strong prediction of this theory.” It is not a prediction of my theory. It is a natural phenomenon. At a given energy (60 MeV in the paper example) the particle velocity will be smaller when the mass is larger (mass = 26.037, B = 0.900931, mass = 0.511, B = 0.99999643). It is not “quite different”: a mass 51 times bigger than the electron mass has a velocity 10% less. It is the same in special relativity: for a particle of rest mass equal to 26.037 MeV the velocity is B = 0.9531055, 5% less. The reviewer continues:
“Using B values from Table II and the dimension of the experiments, it is easy to see that his theory predicts a time difference of as much as 3 to 4 ns in the arrival time of the particles at the detector’s scintillators. Thus his theory predicts a broad time distribution, whereas special relativity predicts a sharp timing distribution. The Crystal Box and Sindrum, with timing cuts of 1.5 ns and 0.8 ns, clearly see narrow timing distribution. This data clearly favors the special relativity prediction and contradicts what Autodynamics predicts.”
Autodynamics does not predict a broad timing distribution, nor does special relativity predict a sharp timing distribution. The time distribution depends only, with the other values constant, upon the kinds of particles participating in the phenomenon. Such particles could be electrons or heavy particles such as electromuons, when there is muon decay. Table II illustrates one example of Autodynamics. The points in Fig. 1(a) are more specific, as will be shown in later examples.
The crystal box and Sindrum devices to not have timing cuts of 1.5 ns or 0.8 ns. The timing cut is determined by the experimenters. When the reviewer is talking about “a time difference of as much as 3 to 4 ns” and “the dimensions of the experiments,” he is referring to the dimensions of the apparatus. The authors of the experiments of Refs. 9 or 6 and 10 in this paper measured time of flight, but they did not mention it explicitly, or the data are not in their papers. The experiments control the time of arrival, but it is impossible to control exactly the time of flight. This is because there is nothing in the target to make it possible to control when the muon decay starts. The drift chamber of ref. 10 does not control the time, it only controls the particle position which determines the particle’s path. The chamber of Ref. 9 is something similar, because it can “determine the coordinate along the cylinder axis.” Of course, it is possible to find the approximate time of flight using this information. In Ref. 10, p. 1417, second column, we read: “The 1.5 ns scintillator timing cut was reimposed after correction of each particle’s time-of-flight for the path length from the vertex to the scintillator,” but is does not seem to be important to the authors, because there is no control of time in the target. What we espoused until now has nothing to do with the authors’ “timing cut” of Refs. 9 and 10 and the “timing distribution” of the reviewer. The particles could be flying for a long path and their arrival time could be 1.5 ns or less if the velocities are comparable. It is necessary not to confuse the two different concepts. The 1.5, 1.1, and 1 are “timing cuts” (see Fig. 10, Ref. 6). The 800 ps or 0.8 ns is not a timing cut; it is a “time resolution” in Ref. 6, p. 12. Figure 2 of Ref. 9 shows the “timing cut” of the events and the solid contour in the central position given the number of events (17) corresponding to a timing cut of -1.5 ns to 1.5 ns. These data do not favor special relativity over autodynamics, because the values have nothing to do with any theory, as was already explained. The experimenters have only tried to reduce the timing cut to be statistically sure that the measured values correspond to a prompt event.
The following examples are given for a plan projection. The hodoscope has an inner radius of 342 mm. A muon decay in three electromuons is a reaction explained in the text regarding the equation mot – mo1 = mos = mo2 + mo3 in which the values are now 106 – 11 = 95 ->88 + 7. The muon decay values are then B = 0.443, 0.997, 0.336; kinetic energy = 1.14, 81.51, 0.51 with kinetic energy sum 83.17, momentum = 4.37, 6.46, 2.44 with momentum sum = 13.28 and with momentum conservation. The faster particle with B = 0.997 supposes a straight path to the hodoscope (which is not true, but will give an extreme value) and has a time of flight of 1.14 ns. The slower particle with B = 0.366, supposing a curved path 1.5 times larger than the hodoscope radius, has a time of flight of 4.617 ns, and the time difference between both is 3.477 ns. With a time difference of 3.5 ns or less, 1.07 x 10^4 events pass this cut (see p. 16 of Ref. 6). With muon decay in three electromuons characterized by 106 – 15 = 91 ->81 + 10, B = 00.512, 0.993, 0.455, kinetic energy sum = 75.31, momentum sum = 19.50 with momentum conservation. The time difference is 2.62 ns.
With muon decay in one electron or positron (20) and two electromuons (44) and (42) characterized by 106 – 20 = 86 ->44 + 42, B = 0.999, 0.872, 0.859, kinetic energy sum = 62.51, momentum sum = 37.72 with momentum conservation. Suppose now that the electromuon is going straight to the hodoscope’s scintillators, and the electron has a curved path length of 1.5 times the hodoscope’s radius, then the time difference is 0.365 ns.
It is noted in Ref. 10 that at a 1.5 ns scintillator timing cut plus other conditions, only 83 events remain, and at a 1 ns interval with cuts of Sum E + | Sum p | 110 MeV and | Sum p | 12 MeV, no events passed these cuts. When the | Sum p | 12 MeV cut was removed, only 11 events passed. The concept of a sharp time difference could also establish a selection rule.
The time difference of 3 ns to 4 ns deduced from Table II caught the reviewer’s attention. From Fig. 17 of Ref. 6 we read: “hodoscope hits coincident within 12 ns” which are given as prompt events in Fig. 16(b), and in Table 3 the same time is given as “majority coincidences (12 ns),” in the same reference (see p. 1416, first column of Ref. 10 and p. 16 of Ref. 6 with 3.5 ns or less).
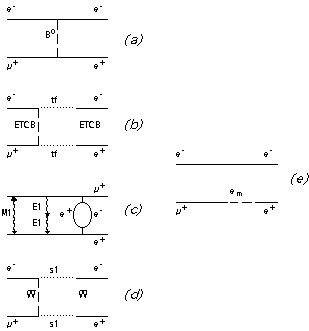 If in Fig. 17(2) of Ref. 6 the “positron” and the “electron” are close to each other, with apparently the same path length and with a time difference of 8 ns (only 2/3 of 12 ns), then this could indicate that the two particles are very different. To have such a long time difference with a short path length, one particle should be moving at a slow velocity. With the path length within the spectrometer of 1.5 times the hodoscope radius (342 mm), the “positron” with B = 0.99999 reaches the hodoscope’s scintillator in 1.7 ns The “electron”, arriving 8 ns later, should move with a velocity B = 0.1763. At this velocity the particle cannot be an electron, because its energy (0.0081 MeV) is too small to be detected (its radius of curvature will be very small). At that small velocity only a heavy particle can satisfy all the conditions, accepting what we tacitly accepted: one unit of electric charge per particle.
If in Fig. 17(2) of Ref. 6 the “positron” and the “electron” are close to each other, with apparently the same path length and with a time difference of 8 ns (only 2/3 of 12 ns), then this could indicate that the two particles are very different. To have such a long time difference with a short path length, one particle should be moving at a slow velocity. With the path length within the spectrometer of 1.5 times the hodoscope radius (342 mm), the “positron” with B = 0.99999 reaches the hodoscope’s scintillator in 1.7 ns The “electron”, arriving 8 ns later, should move with a velocity B = 0.1763. At this velocity the particle cannot be an electron, because its energy (0.0081 MeV) is too small to be detected (its radius of curvature will be very small). At that small velocity only a heavy particle can satisfy all the conditions, accepting what we tacitly accepted: one unit of electric charge per particle.
Hundreds of calculations like this and others with different concepts were made, which encouraged us to prepare the muon decay paper. Because of the time differences found in a large number of experimental events, the idea was favored that particles heavier than electrons are participating in muon decay. [See Fig. 15(b) of Ref. 6 with 8835 prompt events.] The problem is now in the hands of experimenters.
Received 19 April 1990.
Endnotes
{1} The autodynamics equations are the results of a discussion of frames in relative movement, which after a reduction to a “system,” reduce to a simplification of the Lorentz equations which take the following form:
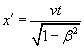
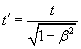
Even though the Autodynamics equation for kinetic energy applies when there are autotransformations of mass into energy, that is, decay, the equation can also represent the kinetic energy equation when the particles receive external energy. An actual version of the “Fundamental Bases for A new Relativistic Mechanics, Autodynamics” is in preparation, because the other, published in 1951, is now impossible to obtain.
{2} The paper was written by Noyes. Waltz was technically responsible for the experiment, and Carezani was the proponent of the Autodynamics theory and only participated in writing the short explanation about the theory and discussing the experiment with the former. Unfortunately, the conclusion espoused by Noyes is irrelevant, because the electron receives the energy from the exterior medium (the klystron electromagnetic field), and the results confirm, two orders of magnitude greater, the Bertozzi experiment, and of course, the special relativity kinetic energy equation. It is therefore impossible to compare one theory to the other, because Autodynamics applies for decay cases. Unfortunately, many other physicists seem to commit, or repeat, the same error. Fortunately, they recognize the error when it is pointed out.
{3} Although the Autodynamics electric charge variation equations is part of this general concept, the equation was first obtained empirically through the experimental variation of the mass-to-charge ratio when the particle receives exterior energy and it electric charge is constant. We might apply the Autodynamics equation when the phenomenon exists, but the phenomenon does not exist because Autodynamics exists.
Ricardo L. Carezani.
References
- Jeremy Bernstein, Science Digest (Aug. 1~). pp, 6, 41.
- G. Auriemma, Y. Srivastava, and A. Widom, Phys, Left. B195, 254 (1987).
- D.R. Walz, H.P. Noyes, and R.L. Carezani, Phys. Rev, A29, 2110 (1984).
- William Bertozzi, Am. J. Phys. 32, 551 (1964).
- G.E. Fisher and Y. Murata, Nucl. Instrum. Methods 78, 25 (1970).
- W, Bertle et al. NucI. Phys. B260, I (1985). This reference was provided by one of the two referees.
- D.A. Bryman and E.T.H. Clifford. Phys. Rev. Lett. 57, 2787 (1986).
- R. Eichler et al. Phy. Lett. B175, 101 (1986).
- W. Bertl et al. Phys, Lett. B140, 299 (1984).
- R.D. Bolton et al., Phys. Rev. Lett. 53, 1415 (1984).
- Phys, Lett. B170, 1 (1986).
- D.A., Bryman et al, Phys. Rev. D33, 1211 (l986).
- M.C. Enderson, Phys Rev. 58, 774 (1940),
- M.H. Kanner and H.H.Barshall, Phys. Rev. 57, 372 (1940).
- J.D. Stranathan, “The Particles” of Modern Physics (Blakiston, Toronto, Philadelphia, 1948), p. 449.
- L Meltact and W Orthmann, Zeit. Phys. 60, 143 (1930); C.D. Ellisand W.A. [¢Cbos~r]. Proc. Soc London 117, 109 (1927),
- R.L. Carezani. Phys. Essays 1, 269 (1988).
- J.S. Allen, Phys. Rev. 61, 692 (1942)