The Sommerfeld Fine Structure
by Ricardo Carezani
Sommerfeld applied SR assuming that the electron inside the atom is traveling near the speed of light. The KE is the already known SR KE equation, where 
is the following expression
(12)
We cannot define the momentum pi conjugate of the variable qi as equal to the derivative of KEwith respect to q.i.
We need to introduce the Lagrange relativistic function
(13)
where U is the potential energy. Now we need to define the following expression
(15)
In the hydrogen atom, the potential energy is independent of q.i, and consequently we can write
(16)
(17)
The conditions (7) for quantification are:
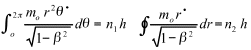(18)
A detailed study of the trajectory led Sommerfeld to demonstrate that the electron precesses around the nucleus.
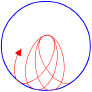
Figure 2
The momentum p
is merely the momentum of rotation around the center and is constant, that is, the theorem of areas is valid.
The first equality in (18) gives
(19)
The total energy is the electron rest mass plus the KE and the potential energy given by
(20)
Taking into account equations (12), (16) and (17) it is easy to verify that W can be written as
(21)
The total energy is conceptually equal to that of classical mechanics, W = E + mo c2, whereE is the kinetic energy and mo c2 the rest mass energy. Resolving equation(21) with respect to pr, we have
(22)
Where A, B and C are written
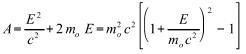
(23)
Sommerfeld introduced, for the first time, what is called the fine-structure constant
(24)
With this, we can write C as follows
(26)
Applying the theorem of residues, we have
(27)
Equating the second member to n2 h according to equation (18) and replacing A, B and C with their values, Sommerfeld found, after a simple calculation
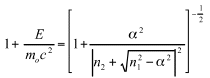(28)
This equation gives the energy E of the ground state defined by the quantum number n1 and n2. Since we are not making a detailed and specialized study of this issue, we only add that the first approximation with no degree greater than 
2 will only find the equation (11). A better result will be obtained if the term in2 is developed to the second degree. If c is replaced by its values from the equation (24) and reworking the term as a sum, the final equation for E is
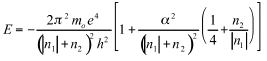(29)
The third term inside the brackets explains the fine structure of Balmer’s series, because the term separately depends on |n1| and n2 , not only on |n1| + n2.
Sommerfeld called n1 + n2 the total quantum number n. Setting n1 = k and taking
(30)
where R is the Rydberg constant, equation (29) is
(31)
Go to next section–> Autodynamics Approach