DISCUSSION: Energy Loss by Electrons in Absorber
by Ricardo L. Carezani
Abstract
For many years a considerable number of experimenters have reported that the energy loss by electrons traversing absorbers of heavy nuclei is larger than the energy calculated from the well-established Bethe-Heitler theory considering together energy loss by collision and radiation. This is particularly true when only the radiation is considered. The phenomenon is far from an explanation accounting for the electrons stopped by the absorber.
To account for the excess of energy loss, many authors suggested the emission of neutrinos, but as was overwhelming proved experimentally by Buechner and van de Graaff there was no energy carried away by neutrinos or other penetrating radiation.
For the first time, this phenomenon is explained by a general theory. This theory also explains all decay phenomena without neutrinos, including muon decay, RaE decay, electron capture, the smaller Linear Momentum Transfer (LMT) in nucleus-nucleus collision, anomalous mean pass, electron-electron and proton-proton annihilation, as well as offering a Compton Effect equation more complete than the classic one.
Introduction
The problem of energetic electrons (beta-rays) between 0.5 and 17 MeV (1’4) striking a target of thin laminated material was studied theoretically and experimentally from 1915(*) to 1956. Later, the subject matter disappeared from the literature without any convincing scientific explanation of the phenomenon, although many prestigious researchers participated in it: H. R Crane (1,4), Chadwick (5), Bethe and Heitler (6), J. Oppenheimer (7), Champion (8), Ellis and Wooster(9).
The experimental results show that the energy loss by scattering of beta-rays inside materials of heavy nuclei is larger than the combined values of collision and radiation given by the Bethe-Heitler formula.
The phenomenon is characterized by two different considerations: electrons losing energy traversing the absorber (1’4), and these electrons plus electrons stopped inside the absorber.
It is well known that the Bethe-Heitler equation perfectly accounts for x-ray production in the energy of the experimental range performed. The difference must lie in the scattering by inelastic collision.
In general, the experimental values are 50% greater than the theoretical values. An explanation argues (2,11): “At least part of the difference can be well accounted for by the fact that the actual length of path of an electron in a lead absorber is somewhat greater than the thickness of the absorbers”. This increment is considered to be between 1.25 and 1.75 times the absorber thickness, although these values are empirically given.
The most important idea, or hypothesis, from the historical point of view, related to the actual state of the neutrino problem was given in the following statement(12).: “To account for extra energy loss, Klarman and Bethe and Champion have suggested the emission of neutrinos, as well as x-rays. Nevertheless, Buechner and Van de Graaff found that the experimental conclusion is overwhelming against the neutrino emission” (12): “experiments using beryllium, gold and mercury targets show that within the experimental error, which is somewhat less than one percent of the energy is carried out of the calorimeter by neutrinos or other penetrating radiation. It thus appears that the production of such radiation cannot account (13) for the large extra energy losses reported from cloud chambers experiments. This also was demonstrated by researchers in the USSR (14).
Special Relativity and Autodynamics
The explanation given in this paper for the phenomenon is not either particular or special for this case.
The theory, the concepts and the equations used to explain the energy loss by inelastic scattering in laminated material of heavy nuclei are general, and the same theory was used to explain all decay phenomena without neutrinos and other phenomena where the neutrino cannot be used or was not used at all.
As is very well known, Pauli invented the neutrino because of an apparent failure of energy and momentum conservation when the special relativity (SR) equations were applied to RaE (83Bi 210) decay. It is also very well known that SR without neutrinos fails to explain all decay phenomena, electron-electron – and especially proton-proton annihilation, anomalous mean pass, and the smaller Linear Momentum Transfer (LMT) found in nucleus-nucleus collision.
The Autodynamics theory (15) can explain all decay phenomena, such as RaE (16), muon decay(17), LMT in nucleus-nucleus collision (18), electron-electron and proton-proton annihilation (19), as well as offering a new equation for the Compton effect (20) more complete than the classic one found with SR.
The Autodynamics equations (21) for Kinetic Energy (KE), momentum (p) and mass variation (mv) are:
KE = mo c^2 [1 -(1-B^2)^1/2] (1)
mv = mo (1-B^2)^1/2 (2)
p = mo (1-B^2)^1/2 B = mv B (3)
Where B=v/c. v=particle velocity. c-light speed. The Autodynamics equations (22) apply especially to decay processes, though they also encompass the case when the particle receives external energy. In a word, the SR equation for KE is a subset of AD theory.
If we write M=mo c^2, we have equation (1) for AD KE equation. If we write M=mo c^2 + KE, is to say, the particle rest mass plus an external energy given to the particle, equation (1) will be:
KE = (mo c^2 + KE) [ 1 – (1-B^2)^1/2 ] (4)
(mo c^2 + KE) (1-B^2)^1/2 – mo c^2 (5)
KE (1-B^2)^1/2 = mo c^2 – mo c^2(1-B^2)^1/2 (6)
KE = mo c^2 [(1-B^2)^1/2 – 1] (7)
The classical SR KE equation.
Scattering and Autodynamics
Although the subject matter was studied by many authors, with similar results, the most commonly used equations are those found by Bethe and Heitler(10).
Equation (49) on page100(21) will be used for collisions
dEo Eo^3
(—–) = 2 D ro^2 mo c^2 Z N log ———– (8)
dx Coll &nbsnbsp; 2 mo c^2 ^2
where ro=e2/mo c^2 is the electronic radius, e-electric charge, moc^2 is the electron rest mass energy in MeV, Z is the element’s atomic number, N is the number of atoms per cm^3, E0 is the primary electron energy in MeV, I is 13.5 Z in MeV, where the number 13.5 for this equation is the observed energy loss of fast a-particles in gold.
We use the equation for radiation (46) on page 98:
dEo Z^2 2 Eo
(—–) = N —- ro Eo (4 log —— – 4/5) (9)
dx Rad. 137 mo c^2
In the radiation case, the most important role is played by the electron energy, but in the collision case, the most important role is played by the electron momentum: when the momentum decreases, the energy loss increases. The AD momentum is many times smaller than the SR momentum.
In SR, the momentum increases with increasing velocity, but fundamentally by increasing mass.
Even though in AD the mass decreases in all decay phenomena, the momentum increases at the beginning until 0.7 of c, then decreases to 0 when v is equal to c because the mass decremented to zero.
In the phenomenon analyzed in this paper, the electrons traversing the absorber are not decaying electrons, and their mass in motion is equal to the rest mass and equation (3) become:
p = mo B (1O)
This values are given in column PA of Table I.
It is possible to see in Table I that the average AD momentum is many times smaller than the average SR momentum in the energy interval considered.
If we take the logarithm of the average KE squared, dividing it by the average AD momentum squared, the resulting value is close to the APR/APA ratio.
With this result applied conceptually to equation (8) the new equation is:
dEo Z N Eo^6
(—–) = 2 D ro^2 mo c^2 —– log ———— (11)
dx Coll-AD p^2 2 mo c^2 I^2
This equation gives curve A in Fig.1 which represents the real phenomenon of electrons striking laminated materials of heavy nuclei with electrons losing energy traversing the material and other electrons stopped inside the absorber. To represent the particular case of only electrons losing energy traversing the absorber, the equation is:
where p2 in equation (10) is replaced by p and its representation in Fig. 1 is curve B.
dEo Z N Eo^6
(—–) = 2 D ro^2 mo c^2 —– log ———— (12)
dx Coll-AD-L p 2 mo c^2 I^2
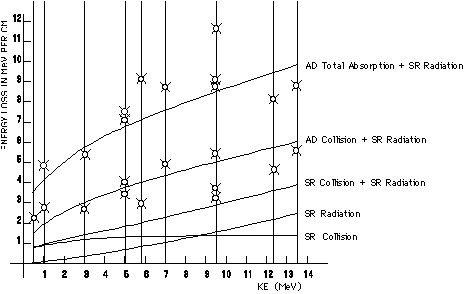
The square points represent our calculated values, extrapolated from the mentioned papers and using Table II of reference (2).
It is clearly visible that curves A and B represent the average experimental values found.
Conclusion
After 50 years of research by the most prestigious experimenters and theoretical physicists, the phenomenon of electron energy loss in thin laminated material of heavy nuclei, is simply and elegantly explained for the first time by a general theory of relativity.
The important experimental conclusion given by Buechner and Van de Graaff, that no neutrinos or other penetrating radiation participate in the phenomenon, validate the AD equations when they are applied to other decay phenomena, which they also explain without neutrinos.