Wilson and Sommerfeld Elliptic Orbits

by Ricardo Carezani

Due to many theoretical considerations, Wilson and Sommerfeld concluded that the Bohr theory was incomplete, proposing to apply the Classical Mechanics to the Keplerian elliptical orbiting electrons, where the values are functions of two variables, r and .

The KE is

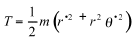(4)

and the Lagrange momenta are by definition

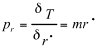(5)

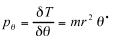(6)

The conditions of quantification are

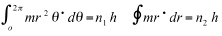(7)

m r2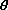 is the momentum of rotation in a central electrical field, in agreement with Kepler’s law of areas, and is coincident with the Bohr condition for circular orbits. To calculate the second integral, we need to take into account the expression for the energy

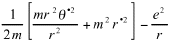(8)

Using the first equation in (7), we have

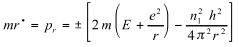(9)

This equation shows the variable separation. Sommerfeld calculated the integral by the Cauchy residues method and found the following value

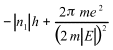(10)

Equating this to n2 h, he found

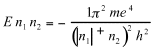(11)

Considering that the term n1+n2could be equal to n, because each is an integer that cannot be simultaneously zero, the theory then gives the same level of energy as the Bohr theory. The introduction of two levels of freedom cannot by itself explain the fine structure of the Balmer series.

Go to next section–> Sommerfeld Fine Structure