by Ricardo Carezani
Until 1912, when Bohr systematically applied the law of mechanics to the spectral term of the hydrogen atom, the issue was treated in part empirically and in part theoretically. Lord Rutherford’s (1871-1937) suggestion to adopt the planetary model as the model for the atom was followed by most physicists. With the Balmer series, the Rydberg constant, the work of Lyman in the ultra-violet and the Pachen series for the infra-red, the spectrum was covered successfully. Of course, from the experimental point of view, this formalism was insufficient.
Bohr’s theory, with its mathematical treatment of the problem, opened the way for further studies.
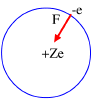
Figure 1
Bohr applied, for the first time, Planck’s idea of quantification. The electron orbit must be an integer multiple of the Planck quantum of action, equal to h/2
. AD students must scrutinize this idea carefully. What Bohr quantified were the energy and the momentum of orbital motion. Quantum Mechanics discusses not a quantum of energy, but a quantum of action of the electron orbital motion. The various orbits of the electron are quantified, depending on the energy it absorbs or emits. This distinction is critical, because many professionals of the Conventional Wisdom hold that Quantum Mechanics describes a quantum of energy for an independent particle. Of course, the energy that atoms absorb or emit will also be quantified, but only as a result of quantum orbital motion.
Bohr, applying the classical mechanics, proposed the two following relations:
(1)
m = electron mass, r = radius orbit, n = integer number and = rotation angle.
as an expression of the quantification of the Planck action. The other equation is:
(2)
wheree = electron electric charge.
The frequency of spectral lines is
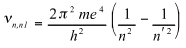(3)
The first term of the right-hand side is sensibly equal to the experimental Rydberg constant.
Go to next section–> Wilson and Sommerfeld Elliptic Orbits