Abstract
There exists a large and impressive literature related to the Cherenkov Effect from the Theoretical and Experimental point of view. This approach only tries to show that Cherenkov’s basic equations can be found starting from the AD’s equations.
Introduction
The application of AD’s equations to Cherenkov’s Effect is a simple conceptual problem. The real difficulty is the proportion between Particle Kinetic Energy converted to Radiation (Electromagnetic radiation, principally Photonic) and the Energy converted, inside the refractive material, to Molecular or Atomic Kinetic Energy. Uncertainty disappears because taking into account Momentum Conservation is what drives AD to the Classical “clear” solution, which does not have the problem of proportionality because any reduction in one parameter automatically reduces the other one in the same proportion.
Momentum in AD.
In AD, momentum, as in Newton, is the product of “mass” times “velocity.”
![]() (1)
(1)
pi = Initial momentum before penetrating the refractive medium, v = particle velocity
In the present case m is the particle rest mass equal to m0 because the particle is not decaying and consequently does not vary.
![]() (2)
(2)
The Photonic emission has a momentum equal to
![]() (3)
(3)
pp![]() = Photonic momentum, N = Number of Photons, h = The Planck’s constant,
= Photonic momentum, N = Number of Photons, h = The Planck’s constant, ![]() = Frequency, c = Light Velocity
= Frequency, c = Light Velocity
Consequently, the equivalent momentum as function of mass is
![]() (4)
(4)
vR = Light Velocity in a Refractive medium.
j being the angle between pm and pi, we have, according to Fig. 1
vR
![]() (5)
(5)
![]() (6)
(6)
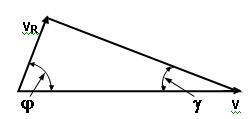 Fig. 1
Fig. 1
Energy Conservation
It is acceptable to apply AD’s Kinetic Energy equation for decay without losing sight of the fact that kinetic energy and mass come from an original particle that decays and provides the particle its actual kinetic energy and mass. But also we remind the reader that AD, starting the derivation from its Kinetic Energy Equation, yields the SR Kinetic Energy Equation where the Kinetic Energy equation is applied to a particle that receives External Energy.
Following the first way above we have exposed:
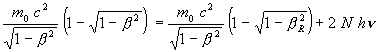
![]() (7)
(7)
Where b = v / c and b R = vR / c
Simplifying
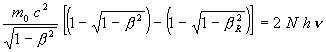 (8)
(8)
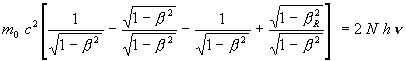 (9)
(9)
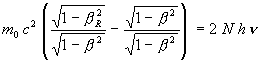 (10)
(10)
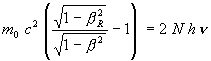 (11)
(11)
Momentum Conservation
The initial momentum m0 v equals the residual momentum m0 vR plus ![]()
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
Remembering equation (5) we have
![]() (15)
(15)
Energy and Momentum Conservation
Equalizing equations (11) and (15), after changing, in equation (11), the velocity b by b n as the valid velocity to calculate the real Kinetic Energy that will be converted to Photonic Energy h n , we have
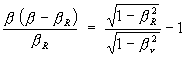 (16)
(16)
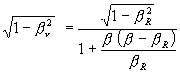 (17)
(17)
 (18)
(18)
![]()
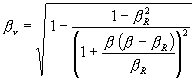 (19)
(19)
The classical equation was found and this solution works perfectly, but given a substantive difference in Kinetic Energy’s proportion to get Photonic Energy when the Refractive Index is larger, even though there are few anomalies regarding n and v, which could drive to impose a “selection rule” in those values beyond the universal condition that v need always to be larger than vR.
Of course more complete research starting from the Energy’s partition is open to AD’s equations regarding the Electrodynamics derived from the Maxwell’s equations applied to the medium where the phenomena happen.